制御工学を学習したことがある方や，ロボティクス関係の方なら誰もが聞いたことがあるはずのPID制御．
今でこそしっかり理解できていますが，制御工学でボード線図やナイキスト線図を使ってPID制御を説明された時はなんのことやらさっぱりでしたw
PID制御を理解するには実験を行うのが最も手っ取り早いと思うので，今回は実験動画を交えながら説明したいと思います！
『PID制御って何？』ってレベルの学生さんも，これを見れば理解できるはずです．
目次
PID制御の目的
PID制御の式を紹介する前に，『PID制御を使って何をしたいのか』という点についてはっきりさせておきます．
そもそも，『制御』とはなんでしょうか？室温が『18度』になるように制御することを考えてみましょう．
この時，できるだけ早く室温を目標温度である18度に設定できれば，良い制御系であると言えますね．
室温を目標温度に設定するためには，『室温を測定する装置』を用意し，現在の室温と目標温度を比較してから送る冷気の量を変えれば良いわけです
PID制御のみならず，『制御』とは，このように現在の測定値と目標値を使って，できるだけ素早く目標値に到達するシステムを設計することと言えます
PID制御とは
PID制御のP，I，Dは以下の3つの英単語の頭文字です．
- P: Proportional 比例
- I : Integral 積分
- D: Differential 微分
後ほど詳しく説明しますが，PID制御とは比例や微分積分の考えを使ったような制御方法ということが名前からもわかると思います．
本記事では，比例項のみのP制御，P制御系に微分項が入ったPD制御，P制御系に積分項が入ったPI制御，そして最後に全てが統合されたPID制御といったように段階的に理解していくような構成にしました．
P制御を理解する
今回は，モータの回転角度を制御する実験を通して，PID制御を説明していこうと思います．
P制御の理論
まずは，一番イメージしやすい比例項のみでできているP制御の式を見てみましょう．
P制御は，回転トルクを\(\tau\)，目標角度を \(\theta_d\)， 現在の角度を\(\theta\)とした時に，\(\tau = K_p(\theta_d-\theta)\)で表されます．
例えば，比例ゲイン\(K_p\)を1とした時，角度が変化するとトルクがどう変化するかを考えてみましょう．
このように，目標角度と現在角度が離れているほどモータの回転が早くなることがわかりますね．
ここから理解できるように，P制御は『目標値と離れているときは大きな入力を与えてモータを早く回転させて，目標値に近づいてきたらゆっくりと調整する』といったような制御法になるわけです
それでは次に，比例ゲイン\(K_p\)を変えてみるとどうなるかを考えてみます．
このように，P制御では比例ゲイン\(K_p\)を上げることでトルクの大きさが変わることがわかります．
言い換えれば，P制御において目標値に早く正確に追従させることができるかどうかは比例ゲイン\(K_p\)の調整にかかっているということ
P制御の実験結果
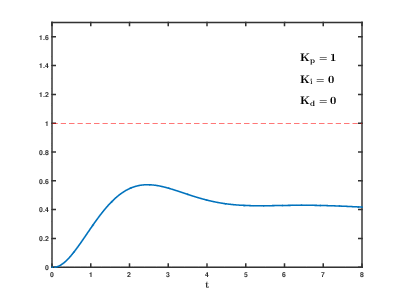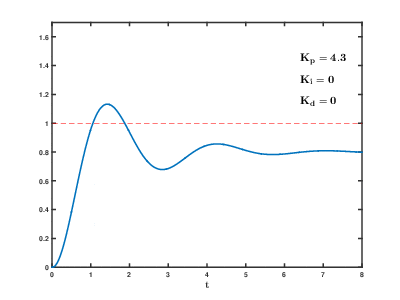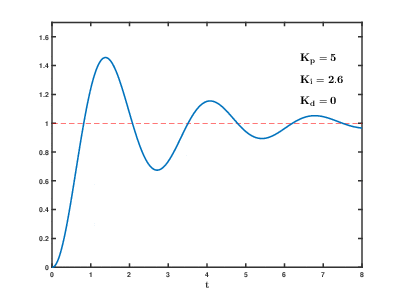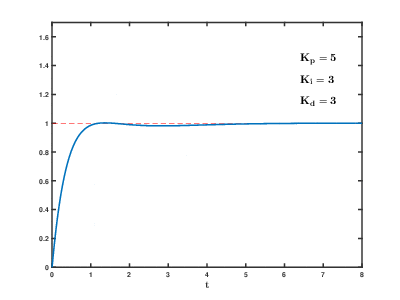
それでは，実際にP制御を行ってみましょう．下の動画が比例ゲイン\(K_p=1\)の時のモータの動きです．
そこそこいい感じに角度制御ができていることが動画からわかると思います．
実験の雰囲気を動画でつかんでもらったところで，グラフを使った議論に切り替えていくことにしますね．
それでは，比例ゲイン\(K_p\)を変えたときにどのような結果になるかをグラフにまとめて見ました．縦軸が回転角度，横軸が時刻を表しています．※下記の『定常偏差』とは，収束状態になった時の目標値と収束した値との誤差のことです！
P制御の特徴をまとめると，以下のようになります．
- 比例ゲイン\(K_p\)が小さいと定常偏差(収束した時の目標値との誤差)が大きくなる
- 比例ゲイン\(K_p\)が小さいと立ち上がり時間が大きくなる
- 比例ゲイン\(K_p\)を大きくするとオーバーシュートが生じる
- 比例ゲイン\(K_p\)が大きすぎる場合，振動現象が発生し収束しない
PD制御を理解する
次は，P制御に，微分要素であるD制御を入れた『PD制御』について理解していきましょう．
PD制御の理論
PD制御は，以下のようにP制御の項と，微分が入ったD制御の項からなります．ぱっと見たところ難しそうに感じると思いますが，『角度の微分に定数をかけたものをP制御から引いているだけ』ということに気づけば拍子抜けするレベル．
では，この『角度の微分×\(K_d\)』というのは何を表しているんでしょうか？
今回の場合，角度の微分は角速度を表しているため，『角速度の定数倍をトルクから引いてあげる』というような意味になるんです．
先ほどの，P制御で比例ゲイン\(K_d\)を大きくしすぎると，オーバーシュートや振動現象が起きてしまっていました．
あれは，\(K_p\)を大きくした結果としてトルクが強くなり，回転が早くなった(=角速度が大きくなった)ために発生してしまった現象だったんです
つまり，角速度に比例した値をトルクから引いてあげれば，行き過ぎや振動現象が起こる可能性が減るということですね？
では，実際に振動現象が軽減されるのかどうかを実験で確認してみましょう．
PD制御の実験結果
D制御を加えることでどのような変化が起きるのかを確認するため，P制御のグラフと，PD制御のグラフを並べてみました．
このように，振動を抑えることができていることがわかります．
PD制御についてまとめると，以下のようになりますね．
- PD制御とはP制御から微分項を引いたものである
- D制御を入れるとオーバーシュートや振動現象を抑えることができる
- 振動現象を抑えられるので，P制御の時よりも比例ゲイン\(K_p\)を上げることが可能
PI制御を理解する
P制御，PD制御と理解してきたところで，次はPI制御について説明して行きます．
PI制御の理論
PI制御は，P制御に積分要素を入れた制御方法で，以下のような式で表されます．
ここで，\(\theta_d-\theta\)は目標角度と現在の角度の差なので，\(\int_0^T(\theta_d-\theta)dt\)は誤差を積分したものであると考えられますね
『誤差を積分したもの』とは具体的にどの部分を表すのでしょうか？
P制御の時のグラフで説明すると，以下グラフの赤色部分の面積が『誤差を積分したもの』を示しています．
この誤差をトルク入力の情報に含めることで，誤差をなくすことができるようになっているというわけですね．
それでは，次に実際に実験してみた結果を確認してみます．
PI制御の結果
I制御を加えることでどのような変化が起きるのかを確認するため，P制御のグラフと，PI制御のグラフを並べてみました．※下記の『定常偏差』とは，収束状態になった時の目標値と収束した値との誤差のことです！
このように，I制御を入れることで，定常偏差(収束した時の目標値との誤差)が0になっているのがわかります．
理論のところで説明したように，I制御を入れると誤差情報をトルク入力に含めるため，誤差をなくすことができるというわけですね
PI制御についてまとめると以下のようになります．
- I制御を入れると，定常偏差を小さく(理論的には0に)することができる
- ただし，I制御を入れると収束に時間がかかってしまう(誤差が蓄積されるのに時間がかかるため)
PID制御を理解する
ここまでの議論で，PID制御の比例，積分，微分がどんな役割をしているかについて説明してきました．
あとは，ここまでのやってきたことを繋げればPID制御になります．
PID制御の理論
PID制御はこれまでに学んできたP制御，I制御，D制御のそれぞれの特徴がわかっていたら簡単に理解できるはずです．
- P制御: 比例ゲイン\(K_p\)を大きくすると立ち上がり時間が短くなるが，大きくしすぎると振動が起こる
- D制御: 微分ゲイン\(K_d\)を大きくすると，振動を抑えることができる
- I 制御: 積分ゲイン\(K_i\)を大きくすると定常偏差を無くすことができる
この3つの制御の特性を理解した上で，\(K_p\)，\(K_i\)，\(K_d\)を調整し，良い制御系を作ることが『PID制御系の設計といえます』
PID制御がわかるgif
PID制御の各ゲインを変えたらどうなるのかを視覚的に理解できる動画を見つけました (引用元)
『なぜこのような変化をするのか』が分かっていればPID制御に関する基本的なことは理解できていると考えて良いはずです．
各ゲインを数学的に求める方法もありますが，本記事はざっくりとPID制御に関して理解してもらうことを目的にしているため，割愛します．
最後に，PID制御のモータ角度制御を使って，ピアノを演奏するおもちゃを作ってみました．下の方の青いレールにくっついているモータにPID制御を利用しています．
そういえば今日の実験でピアノが弾けるようになった pic.twitter.com/IGQZi7HZDk
— 迫 佑樹 (@yuki_99_s) 2017年11月30日
鍵盤が小さいので結構精度がいるんですが，うまく各ゲインを調整するとこれくらいの動きはしてくれます．
実験器具
参考までに，以下のような実験器具を使いました．
やって見たい方は，Arduinoを始めようキットというのがAmazonで売っているので，それに加えてモータと角度計測用のエンコーダを購入すればOKです．
自分でやってみると理解もかなり深まるので，ぜひ一回ご自身で実験してみることをおすすめします！
大学生に人気の記事はこちら！
- 【大学生の8割がクレカを保有する時代】学生向けクレジットカードを紹介！
- 動画サービスの無料期間を駆使して，約半年間無料で動画を見まくる方法
- 大学生なら絶対に知っておきたい投資・資産運用の話
- 【全て実践済み！】大学生がアルバイト以外で稼ぐ20の方法
- 【実体験】大学生の間にやっておいてよかった10のことを全部公開
▼期間限定で無料配布中▼
- 経済的自立を果たす10のステップ
- 時給10円から年商10億円に至る道のり
- 最短で0→1を立ち上げる起業術
- お金持ちになる5つのルール
- すぐに実行できる即金マニュアル
無料特典を受け取るか迷っている方は、こちらの記事「真面目」でも「頭がいい人」でもお金持ちになれないたった1つの理由」をお読みください。
