高校3年生の夏，突如として現れた謎の無理数\(e\)
ネイピア数と呼ばれ，自然対数の底によく出てくる\(e\)
その\(e\)の定義は高校3年生の数学Ⅲの教科書にしれっとこう書いてあります．
$$e = \displaystyle \lim_{x \to 0} \bigl(1+x\bigr)^{\frac{1}{x}}$$
もしくは
$$e = \displaystyle \lim_{x \to \infty} \bigl(1+\frac{1}{x}\bigr)^x$$
私は初めてこれを習った時，「は？どっからでてきたこれ」ってなりましたが，先生は…
これは定義だからこういうものです
覚えましょう
まぁたしかにそうなんですが，定義の背景には，そう定義すれば都合の良い理由があるはずなんですよね．
ということで，この\(e\)の定義について今日は見ていきましょう．
eがよく出てくる所
さて，eがよく出てくるところってどこでしょうか？
そうです，微分ですね．
微分方程式を解いていると，必ずと行っていいほど\(e\)が出てきます．
しかも，理系の方ならおなじみ，\(e\)には，指数関数\(e^x\)を微分した結果は，\(e^x\)とという素晴らしい性質があります．
また，底を\(e\)とする対数関数\(log(x)\)の微分は\(\frac{1}{x}\)ととてもきれいになりますね．
さて，これって，本当にたまたま\(e^x\)や\(log(x)\)を微分した結果こうなったのでしょうか？
いや，きれいになるように自然対数\(e\)を定義したと考えるほうが自然じゃないでしょうか？
ということで，今回は，指数関数や対数関数の微分という観点から，ネイピア数\(e\)の定義を見直してみましょう．
微分の定義を確認してみる
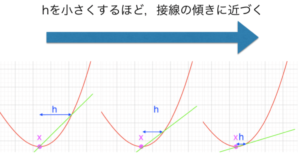
さて，微分という観点から\(e\)の定義を見直してみるのは良いのですが，その前に微分の定義だけ確認しておきます．
関数\(f(x)\)が与えられた時，導関数\(f'(x)\)は，\( \displaystyle \lim_{h \to 0} \frac{f(x+h) – f(x)}{h}\)で定義されます．
微分の定義に関しては，詳しくは扱いません．
気が向いたらまた書きます．
指数関数の微分からeを見直してみる
さて，指数関数の微分を見ていきましょう．
指数関数，\(f(x)=a^x\)を考えてみます．
先程の微分の定義にしたがって指数関数を微分してみましょう．
さて，指数関数の特徴を使うと，\(a^{(x+h)}\)というのは，\(a^x a^h\)と書くことが出来ます．
なので，上の式は
とかけます．
お，都合の良いことに，分子から\(a^x\)をくくりだすことが出来ます．
さらに，\(a^x\)は\(h\)に関係ないので，limの前に出せます．
おぉ？
これって，もとの\(f(x) = a^x\)に\(\displaystyle \lim_{h \to 0} \frac{a^h – 1}{h}\)がかかったものですね．
つまり，\(\displaystyle \lim_{h \to 0} \frac{a^h – 1}{h}\)が1になるような値\(a\)を底とする指数関数は，微分してもそのままで都合がいいになるわけです．
さて，それでは\(\displaystyle \lim_{h \to 0} \frac{a^h – 1}{h}=1\)になるような\(a\)を考えてみます．
\(\displaystyle \lim_{h \to 0} \frac{a^h – 1}{h}=1\)を，\(a\)について解けばいいだけですのでまずは，両辺に\(h\)をかけてあげます．
そして，左辺の1を右辺へ移行
そして，両辺\(\frac{1}{h}\)乗します．
でました， \(e = \displaystyle \lim_{x \to 0} \bigl(1+x\bigr)^{\frac{1}{x}}\)です．
この\(a\)がネイピア数\(e\)の定義であり，こう定義すると指数関数の微分がとても扱いやすいというのがわかってもらえたでしょうか？
対数関数の微分からeを見直してみる
さて，指数関数の微分の時に都合の良いのが\(e\)だというのが上の話でわかりました．
序盤に考えた，「\(log(x)\)の微分が\(\frac{1}{x}\)ときれいになる」についても考えてみましょう
指数関数のときは，底がaの指数関数を考えました．
同様に底がaの対数関数\(f(x) = log_a(x)\)を考えてみます．
これを，定義に従って微分してみます．
対数関数の性質より，以下のように書くことができます．
それを使うと，次のように変形できます．
ちょっと見にくいので，分数を前に出します．
対数関数の性質より，\(\alpha log(x) = log(x)^{\alpha}\)とかけますので，次のように変形できます．
\(log\)の中身を計算します．
logの中に分数があるのが嫌なので，\(\frac{h}{x})\)をなんかの変数で置き換えましょう．
今回は，\(\frac{h}{x})\)を\(t\)と置いてあげます．
すると，\(h=xt\)になります．
また，hが0に近づく時，同じくtも0に近づくので，以下のように変形することが出来ます．
ここで，\(\frac{1}{x}\)を対数の前に出し，\(lim\)の前に出してあげます．
さぁ，見えてきました．
つまり，上の式の後半の\(\displaystyle \lim_{t \to 0} log_a(1+t)^{\frac{1}{t}}\)が1になれば，対数関数の微分がとてもきれいな形になるという話です．
対数の底と真数部分が同じなら，その値は1になります．
つまり，対数の底\(a\)を\(\displaystyle \lim_{t \to 0}(1+t)^{\frac{1}{t}}\)とすれば，導関数が\(\frac{1}{x}\)になって都合が良いというわけ．
ということで，対数の微分を綺麗にするための底eとして，\(e = \displaystyle \lim_{t \to 0} (1+t)^{\frac{1}{t}}\)と定義すれば都合が良い．
まとめ
いかがだったでしょうか？
高校でネイピア数\(e\)が初めて出現したときは誰もが感じたであろうこの疑問．
定義の裏にはしっかり背景があるんです．
「定義だから覚えろ!!」という前に，少しこのような話をまぜると，もやもやがなくなります．
数学関連オススメ
これを読んでくれた方にはこちらの記事もオススメです！
▼期間限定で無料配布中▼
- 経済的自立を果たす10のステップ
- 時給10円から年商10億円に至る道のり
- 最短で0→1を立ち上げる起業術
- お金持ちになる5つのルール
- すぐに実行できる即金マニュアル
無料特典を受け取るか迷っている方は、こちらの記事「真面目」でも「頭がいい人」でもお金持ちになれないたった1つの理由」をお読みください。
